Deep Learning Course Review Notes

Review class video recording GRC and his friends’ notes

0. Question Types

Type	Quantity	Score
Short Answer	4	60
Design	2	25
Unknown Type	1	15

The teacher was quite secretive about the last question, “As long as you listened in class, you could still score some points.”

1. Outline

Chapter Two

• Master the stochastic gradient descent algorithm
• Master the batch gradient descent algorithm
• Understand regularization (L1, L2)
• Master the concept, processing, etc., of Dropout
• Master common theories: NFL, Ugly Duckling, Occam’s Razor, etc.

Chapter Three

• Master Logistic regression, Softmax regression
• Master various common loss function formulas and their applications to specific scenarios, such as square loss, cross-entropy loss, etc.
• Understand empirical risk and structural risk

Chapter Four

• Master the advantages and disadvantages of a few common activation functions (Sigmoid, ReLU)
• Understand the basics of feedforward neural networks

Chapter Five

• Master the features of convolutional neural networks (compared to fully connected networks)
• Convolutional networks: convolutional kernels, feature maps, number of color channels
• The role of the pooling layer
• Calculation of parameters in common typical CNN convolutional structures (for example, the amount of parameters in a convolutional layer, the number of connections, output image size, etc.)
• Master residual networks (working principle, formulas, etc.)

Chapter 6

• Expression of RNN formula
• The problem of gradient vanishing and gradient explosion in RNN
  • Corresponding solutions
• Master sequence-to-sequence models (synchronous and asynchronous)
  • Specific applications (synchronous and asynchronous-Sentiment Analysis)
  • Formula expression
  • Pros and cons
• Master LSTM
  • The functions and meanings of the three gates
  • The pros and cons of LSTM compared to RNN
  • ‘Input and output
  • ‘LSTM can solve the gradient vanishing problem, similar to the treatment method of residual networks
• Master GRU
  • Improvements over LSTM
  • ‘Formula of GRU

Chapter 7 Network Optimization

• Improvements in learning rates
• Learning rate decay-just have a look
• Periodic adjustment-no need to look at the formula
• Focus on mastering: adaptive adjustment: Adagrad, Adadelta, RMSProp
  • Master the formulas and principles of these three methods, focusing on the formulas
• Gradient optimization
  • Momentum method
  • Nesterov accelerated gradient
  • Adam algorithm
• Gradient clipping
• Network optimization in high and low dimensional situations

  Escaping saddle points

• Three methods of data normalization
  • ‘Eliminating correlation between relevant dimensions - whitening
• Master batch normalization and layer normalization (definition, method, specific operation methods)
• Dropout method

Chapter 8

• Master the attention model
  • Significance-why the attention model
  • Formula
  • Processing procedures, etc.
• Master the self-attention model
  • Significance-important to master, improvements over previous, KQV calculations, etc.
  • Formula
  • Processing procedures
• Master Transformer (structure, techniques, etc.)

Chapter 14

• The five elements of reinforcement learning
  • The fifth element: $\pi_s$ policy
• Two value functions: state value function, state-action value function
• Master the policy iteration algorithm, value iteration algorithm, SARSA algorithm, and Q-Learning algorithm

Monte Carlo sampling

2. Overview of Machine Learning

Three Elements of Machine Learning

Model

Linear model Generalized linear model $$f(x;\theta) = w^{T}\phi (x)+b$$

Learning Criterion

In the linear regression model, all the following loss functions $\mathbb L$ are squared loss functions.

Expected risk is in terms of the real-world situation

However, the true data distribution cannot be obtained, and can only be approximated through empirical risk:

When using empirical risk to approximate expected risk, generalization error occurs. To reduce the generalization error, both optimization and regularization (damage optimization, prevent overfitting) methods are needed. Structural risk adds a regularization term on the basis of empirical risk, and the minimization of structural risk can solve (mitigate) the overfitting problem.

Optimization Methods

(Batch) gradient descent, stochastic gradient descent, mini-batch gradient descent, early stopping

(Batch) Gradient Descent

Batch gradient descent method needs to calculate the gradient of the loss function on each sample and sum them up in each iteration (the target function is the risk function over the entire training set). When the number of samples 𝑁 in the training set is large, the space complexity is relatively high, and the computational overhead of each iteration is also large.

Stochastic Gradient Descent

Batch gradient descent is equivalent to collecting 𝑁 samples from the real data distribution, and approximating the gradient of expected risk with the gradient of empirical risk calculated from them. To reduce the computational complexity of each iteration, we can also collect just one sample in each iteration, calculate the gradient of this sample’s loss function and update the parameters, namely stochastic gradient descent

The difference between batch gradient descent and stochastic gradient descent lies in whether the optimization target for each iteration is the average loss function over all samples or the loss function of a single sample. Due to its simple implementation and very fast convergence, stochastic gradient descent is widely used. Stochastic gradient descent is equivalent to introducing random noise to the gradient of batch gradient descent. In non-convex optimization problems, stochastic gradient descent is more likely to escape local optima.

Mini-batch Gradient Descent

Regularization Methods

Regularization is a category of methods that improve generalization ability by restricting the model complexity to avoid overfitting, such as introducing constraints, adding priors, early stopping, etc. The methods of regularization include:

1. L-norm regularization
2. Weight decay
3. Early stopping
4. Dropout
5. Data augmentation
6. Label smoothing

L-norm Regularization

It essentially introduces a constraint as a penalty. Therefore, during optimization, one cannot only focus on the objective function but must also consider the introduced penalty (regularization term).

L1 regularization applies the same penalty to all weights, regardless of their magnitude, resulting in smaller weights becoming zero. This makes the primary effect of L1 regularization to sparsify the model by turning a large number of parameters to zero. L2 regularization imposes a heavy penalty on large weights and a lighter one on small weights. It typically incorporates the square of the L2 norm into the formula for easier calculation (as shown in the images above).

Dropout

See the network optimization - Dropout section for details $$mask(x) = \begin{cases} mx, \quad training\ phase \ px, \quad testing\ phase \ \end{cases}$$

Common Theorems

No Free Lunch Theorem (NFL): For iterative optimization algorithms, there is no single algorithm that is effective for every problem (within a finite search space). If an algorithm is effective for certain problems, it must perform worse on others compared to a pure random search algorithm. That is, the efficacy of an algorithm cannot be discussed without considering specific problems; every algorithm has its limitations. One must “analyze specific problems in detail.”

Occam’s Razor Principle: “Entities should not be multiplied needlessly.” The idea behind Occam’s Razor is very similar to the concept of regularization in machine learning: simpler models have better generalization ability. If two models have similar performances, we should choose the simpler one. Therefore, in the learning criteria of machine learning, parameter regularization is often introduced to limit the model’s capacity to avoid overfitting.

Ugly Duckling Theorem: “The difference between an ugly duckling and a white swan is as significant as the difference between two white swans.” Because there is no objective criterion for similarity in the world, all standards of similarity are subjective. If looked at from the perspective of size or appearance, the difference between an ugly duckling and a white swan seems greater than the difference between two white swans; however, if viewed from a genetic perspective, the difference between the ugly duckling and its parents is less than the difference between its parents and other white swans. Here, the ugly duckling refers to a juvenile white swan

3. Linear Models

Reference: A comparison of two types of linear models

Logistic Regression

Known as logarithmic odds regression in the Watermelon book, it is a commonly used model for binary classification problems

This is a plain linear model: $f(x;w)=w^{T}x$ By introducing an activation function for non-linear transformation, the output is mapped between $[0,1]$, serving as the probability of predicting a positive example: $$p(y=1|x) = g(f(x;w))=\frac{1}{1+exp(-w^Tx)}$$ In essence, the output $f(x;w)$ is the log of the odds ratio of the posterior probabilities of sample x being a positive or negative example: $$w^{T}x = \log \frac{p(y=1|x)}{p(y=0|x)}$$ The loss function uses cross-entropy: $$R(w) = -\frac{1}{N} \sum\limits_{i=1}^{N}(y_{i}\log (\hat y_{i})+(1-y_{i})\log (1-\hat y_{i})) $$ where $y_i$ is the actual value (label), $\hat y_{i}$ is the predicted value The derivative results in a multiplication of input and first-order loss, thus gradient descent update as follows: $$w_{t+1} = w_{t}+ \alpha \frac{1}{N} \sum\limits_{i=1}^{N}x_{i}(y_{i}-\hat y_{i})$$

Softmax Regression

A general form of Logistic regression for multiclass classification

Regularization is added to the risk function to constrain its parameters. Failing to limit the size of the weight vector with regularization could lead to excessively large weight vectors, causing overflow.

Analyzing why the squared loss function is not suitable for classification problems. In classification problems, labels do not have a continuous concept. The distance between each label is also meaningless, so the squared difference between the predicted value and the label vector cannot reflect the degree of optimization for the classification problem.

For example, in classifying 1, 2, 3, if the true category is 1, being misclassified as 2 or 3 should be considered equally wrong, but the squared loss function would yield different loss values.

①Objective inconsistency: The goal of classification problems is to correctly classify samples into different categories, not to predict a continuous value. The squared loss function aims to minimize the squared difference between predictions and actual values, which is inconsistent with the goal of classification problems. ②Sensitivity to outliers: The squared loss function is very sensitive to outliers. In classification problems, outliers usually represent misclassified samples, meaning that incorrect classification of outliers leads to very high loss. Outliers are more common in classification problems because they involve predicting discrete category labels, and outliers can lead to larger errors. ③Vanishing gradient: The squared loss function can lead to vanishing gradient issues in classification problems. Since the output of classification problems is a probability or category label, when using the squared loss function, the gradient may become very small, making it hard for the model to learn or converge. ④Non-differentiability: In classification problems, commonly used activation functions (such as sigmoid, softmax) are usually incompatible with the squared loss function. This is because the output produced by these activation functions is not continuous, while the squared loss function is differentiable for continuous outputs. Therefore, using the squared loss function in classification problems might result in non-differentiability, preventing the use of standard optimization algorithms for training.

4. Neural Networks

Activation Functions

A qualified activation function should possess the following properties:

• Continuously differentiable
• Simple and convenient for computation
• Value range within an appropriate interval

Sigmoid Series

Both are sigmoid functions, characterized by saturation:

• High computational cost
• Smooth output, no jump values
• Differentiable everywhere
• Suitable for probability
• Gradient vanishing
• Centered at 0/ Not centered at 0

ReLU Series

Advantages - Low computational cost, involving simple addition and multiplication - Biologically plausible: unilateral inhibition - Saturation on the left side, the derivative is 1 for x>0, alleviating gradient vanishing - Accelerates the convergence speed of gradient descent Disadvantages Non-zero centering, biases the later layers Dying ReLU problem: an improper update can permanently deactivate it (ELU can solve this)

Feedforward Neural Network

The input layer is not counted in the number of network layers; the number of network layers refers to the number of hidden layers

Universal Approximation Theorem

According to the Universal Approximation Theorem, for feedforward neural networks that have a linear output layer and at least one hidden layer using an “squashing” activation function, as long as the number of neurons in the hidden layer is sufficient, it can approximate any function defined on a bounded closed set in the real number space with arbitrary accuracy. Neural networks can be used as a “universal” function for complex feature transformations or to approximate a complex conditional distribution.

5. CNN

The following problems are associated with processing images using FCN:

• Too many parameters
• Lack of local invariance Objects in natural images exhibit local invariance characteristics, such as scale zooming, translation, rotation, etc., which do not affect their semantic information. It is challenging for fully connected feedforward networks to extract these local invariance features.

Characteristics of CNN

CNNs are inherently suitable for processing images:

1. Local connectivity: Local connectivity significantly reduces the network parameters. When dealing with high-dimensional inputs like images, it is impractical to fully connect each neuron to all neurons in the previous layer. By connecting each neuron only to a local region of the input data, the spatial size of this connection, called the neuron’s receptive field, is a hyperparameter, which is essentially the spatial size of the filter.
2. Weight sharing: Parameter sharing in convolutional layers is used to control the number of parameters. Each filter is locally connected to the preceding layer, and all local connections of each filter use the same parameters, which also greatly reduces the network parameters.
3. Spatial or temporal subsampling: Its role is to gradually reduce the spatial size of the data, thereby reducing the number of parameters in the network, lessening computing resource consumption, and effectively controlling overfitting. These characteristics endow convolutional neural networks with a certain degree of translation, scaling, and rotation invariance. Compared with feedforward neural networks, convolutional neural networks have fewer parameters.

Convolutional Layer

Kernel size: The convolution kernel defines the size range of the convolution, representing the size of the receptive field in the network, with 3*3 convolution kernels being the most common. Generally, the larger the convolution kernel, the larger the receptive field, the more image information seen, and the better the global features obtained. However, large convolution kernels lead to a surge in computational demand and a decrease in computing performance. (Extremely large becomes FCN) Stride: The stride of the convolution kernel represents the precision of extraction. Stride defines the length crossed every time the convolution kernel convolves over the image. For a convolution kernel of size 2, if the step is 1, there will be overlapping regions between adjacent steps; if the step is 2, there will be no overlap or uncovered areas between adjacent receptive fields; if the step is 3, there will be a gap of 1 pixel size between adjacent steps, which, in a way, misses the original image’s information. Padding: A mismatch between the convolution kernel size and the image dimension results in the post-convolution image differing in size from the pre-convolution image. To avoid this situation, it’s necessary to perform edge padding on the original image first.

Feature Map: A feature map is the feature extracted from an image (or another feature map) after convolution. Each feature map can serve as a type of extracted image feature. To enhance the representational ability of convolutional networks, multiple different feature maps can be used at each layer to better represent image features. At the input layer, the feature map is the image itself. For a grayscale image, there is one feature map, with the input layer’s depth 𝐷 = 1; for a color image, there are RGB three color channel feature maps, with the input layer’s depth 𝐷 = 3. The input feature map of the convolutional layer is $M \times N \times D$, and the output is $M’ \times N’ \times D’$, each output feature map requires 𝐷 convolution kernels and one bias. Assuming each convolution kernel size is 𝑈 × 𝑉, then a total of 𝑃 × 𝐷 × (𝑈 × 𝑉) + 𝑃 parameters are needed. Convolution output image size: $$M’ = \frac{M-K+2P}{S}+1$$ Number of connections: Number of parameters × Output feature map plane size $(M’ \times N’)$

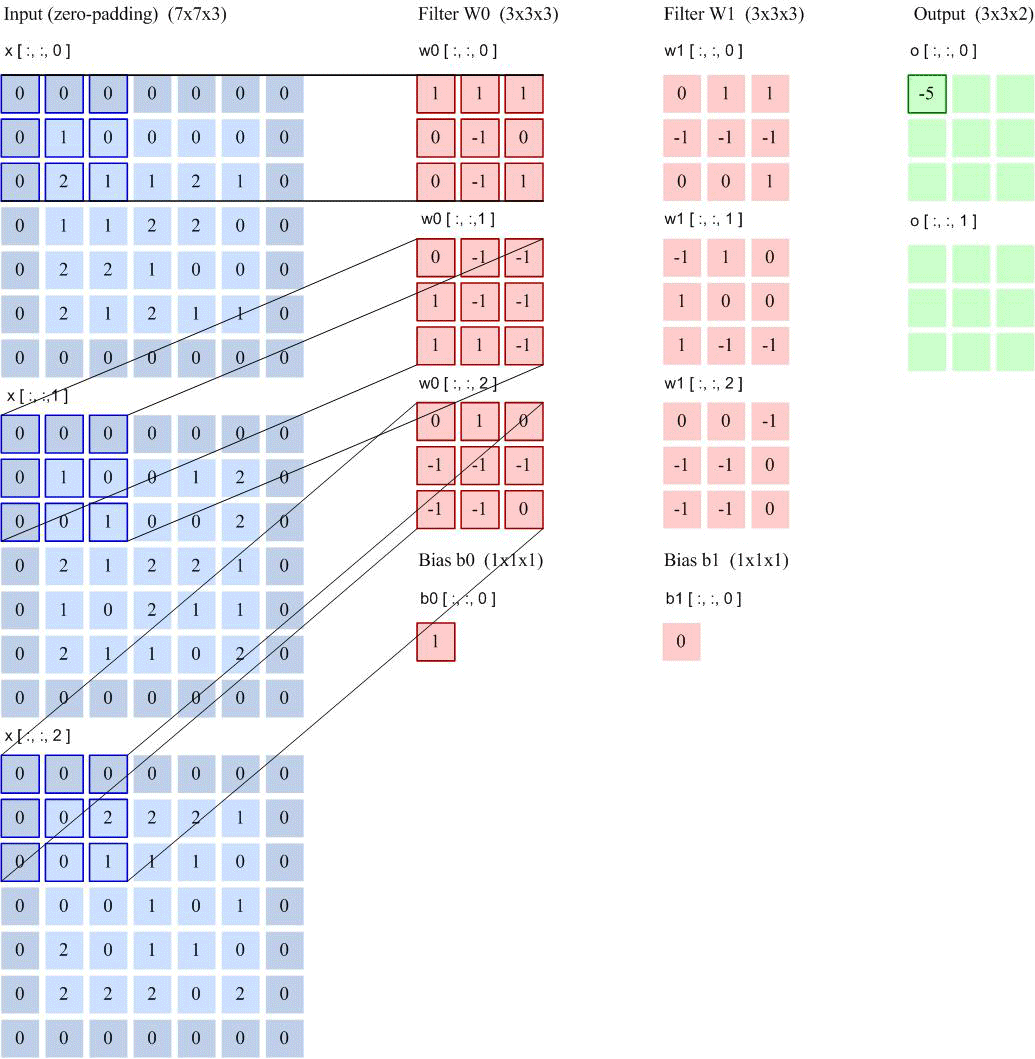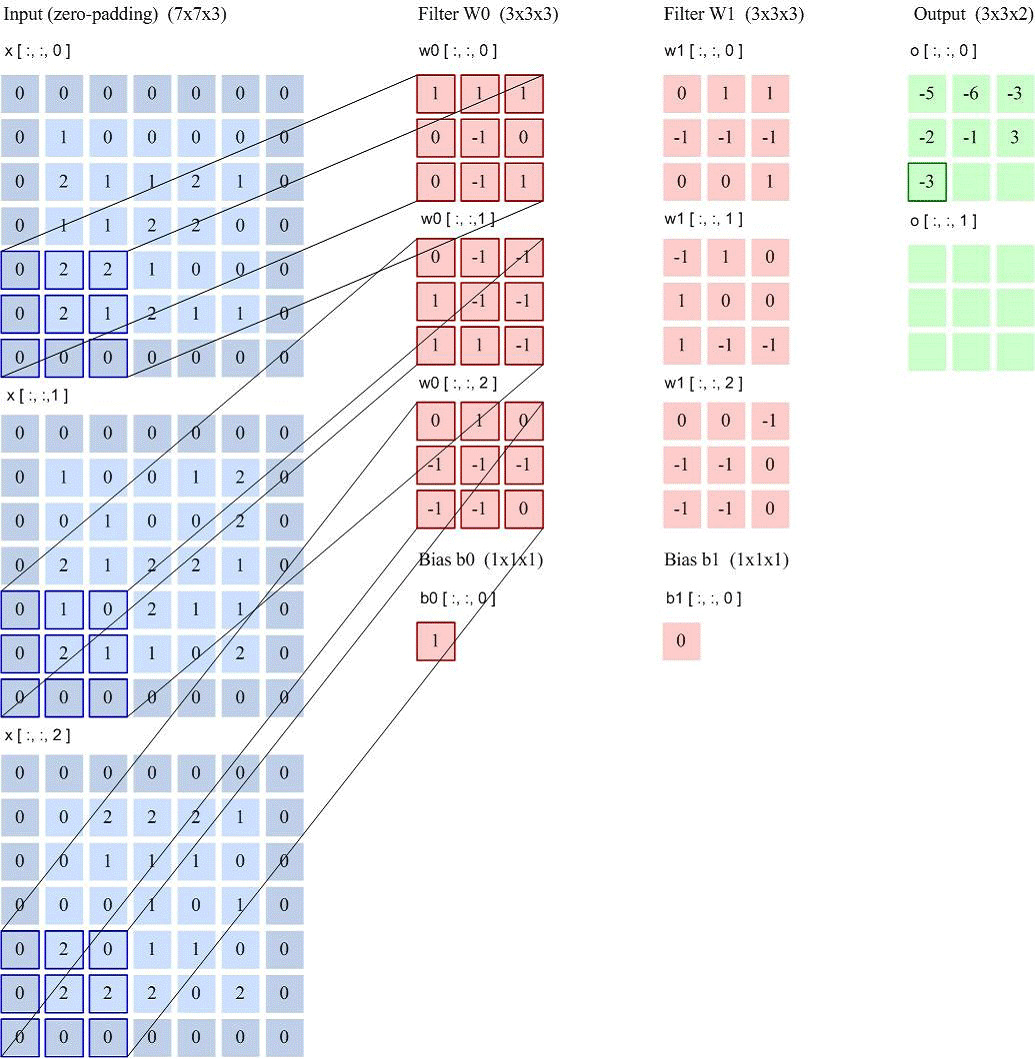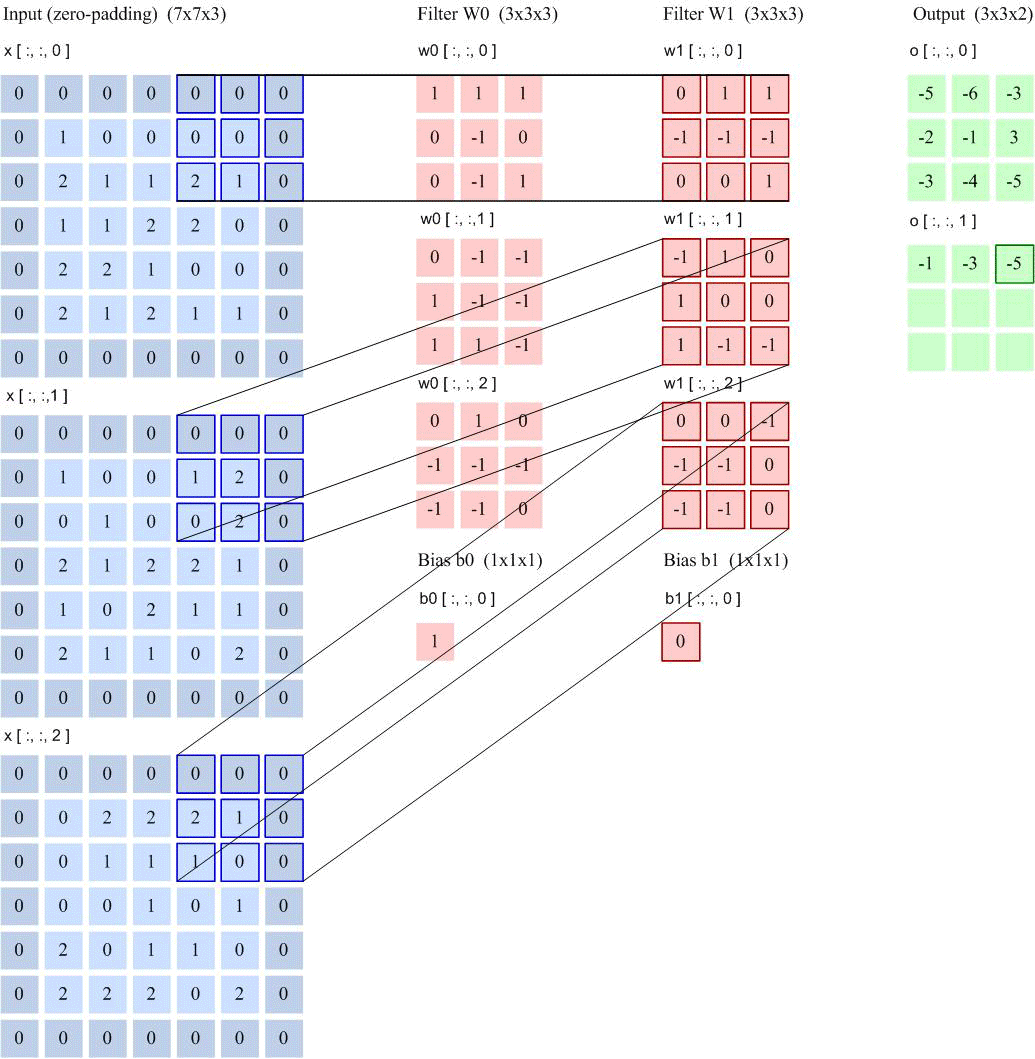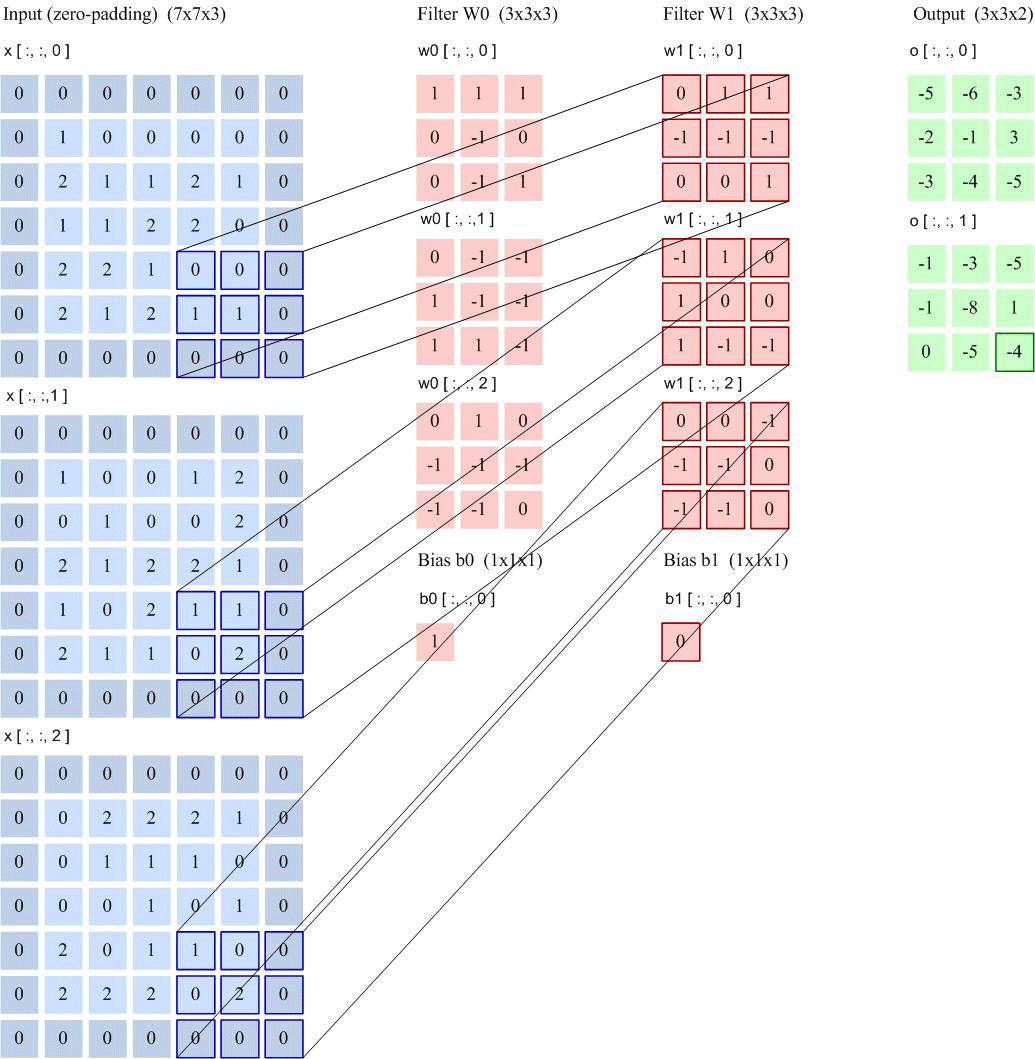
Taking LeNet-5 as an example for calculation:

Pooling Layer

Purpose:

1. Reduce computation and the number of parameters, making the model easier to train;
2. Lower the resolution of feature maps, reducing overfitting;
3. Extract more important features, because the pooling layer selects only the maximum or average values, which often contain more information.

Residual Network

Question

Analyze the function of using 1 × 1 convolution kernels in convolutional neural networks.

Answer

1. Dimension Reduction (Reducing Parameters) In the Inception network 1 × 1 convolutions are used to reduce the depth of feature mappings.
2. Dimension Increase (Expanding dimensions with minimum parameters) As shown in this ResNet network structure The right side’s last layer uses a 1 × 1 × 256 convolution kernel to increase the output dimension from 64 to 256 and it requires only 64_1_1*256 parameters.
3. Cross-channel information interaction The processes of reduction and increase in dimensions are actually linear combinations across different channels, which is the essence of cross-channel information interaction.
4. Adding Non-linearity Each convolution operation is followed by a non-linear activation function, enabling 1 × 1 convolutions to add non-linearity without altering the scale of the feature map.

6. Attention Mechanism

Due to the limitations of optimization algorithms and computing power, to achieve universal approximation capacity, the network cannot be too complex.

Attention

Significance

Addresses issues of long-sequence semantic loss and input contribution distribution.

1. Source is processed through an Encoder, generating an intermediate semantic encoding C.
2. C is then processed by a Decoder, producing the translated sentence. In recurrent neural networks, y1 is generated based on C, then y2 is based on (C, y1), and so on. In traditional recurrent neural networks, the calculations for y1, y2, and y3 are all based on the same C. However, this might not be the best approach, as different words in Source have varying impacts (contributions) on y1, y2, and y3.

Starting with semantic encoding C, the attention mechanism allows it to adaptively change at each moment according to the inputs of the encoder, thus influencing the output of the next module (e.g., the decoder). AIM: To address the problem of contribution level of each input

Formula

Process

1. F(Q,K) calculates similarity, options include Dot Product, Cosine, MLP
2. The output of F is then normalized through Softmax to obtain the attention allocation probabilities
3. Finally, calculate the weighted average of the input information based on $a_i$ to obtain the attention value There’s not much difference from the previous figure, it’s more concise and intuitive. It is worth noting that the weighted average after SoftMax can be written in the form of the expectation of random variables.

Variations

This is the key-value pair attention mechanism as discussed by Li Hongyi.

Multi-head attention mechanism.

Self-Attention

Meaning

Introducing the Self-Attention mechanism, as the name suggests, refers to the Attention mechanism that occurs between the elements within the Source or within the Target, or can be understood as the special case where Source = Target. The specific computation process is the same as that of Soft Attention.

KQV Model

Exactly the same as explained by Li Hongyi. The processing in SoftMax is slightly different, where the denominator is a constant.

Process

1. Calculate the $k,q,v$ vectors, which are obtained by multiplying the input $X$ with the corresponding weight matrices $W^K,W^Q,W^V$
2. Calculate self-attention by dot product of Query and Key, which determines the degree of attention to other parts of the input sentence when encoding a word in some unknown location
3. Divide the dot product result by a constant (usually $D_k=64$), then apply softmax to it. The resulting values indicate the relevance of each word to the current location word (maximum with itself)
4. Multiply and add the Value with the softmax obtained value. The result is the value of self-attention at the current node (scaled dot-product attention)

Transformer

Structure

The transformer adopts an encoder-decoder architecture, as shown in the figure. The Encoder layer and Decoder layer are each composed of 6 identical encoders and decoders stacked together, making the model architecture more complex. Among them, the Encoder layer introduces the Muti-Head mechanism, which can be computed in parallel, while the Decoder layer still needs to be computed serially.

Show-off Techniques

• Self-attention: Calculates the association of every word in the sentence with other words, helping the model to better understand the context semantics

• Multi-head attention: Each head focuses on different parts of the sentence, enhancing the Attention mechanism’s expression ability of the impact between words within the sentence Why does the Transformer need Multi-head Attention? The original paper states that the reason for using Multi-head Attention is to divide the model into multiple heads, forming multiple subspaces, allowing the model to pay attention to different aspects of information, and then integrating all aspects of information together. Intuitively, multi-head attention helps the network to capture a richer set of features/information.

• Feedforward Neural Network FFN: Introduces a nonlinear transformation to the encoder, enhancing the model’s fitting ability.

• The Decoder accepts output input while also receiving encoder input, helping the current node to focus on the content that needs attention.

• Feed Forward Network: After each layer goes through attention, there will be an FFN, which serves the purpose of spatial transformation. FFN consists of 2 layers of linear transformation with ReLu as the activation function in between. The inclusion of FFN introduces nonlinearity (via the ReLu activation function), changing the space of the attention output, thereby increasing the model’s expressive power. Removing the FFN would still allow the model to function but with significantly diminished effectiveness.

$$FFN(x) = ReLU(xW_{1}+b_{1})W_{2}+b_{2}=max(0,xW_{1}+b_{1})W_{2}+b_{2}$$

• Layer Normalization: Regulates and optimizes space, speeding up convergence.

$$LN(x_{i})=\alpha \frac{x_{i}-\mu_{i}}{\sqrt{\sigma^{2}+\xi}} + \beta$$

• Positional Encoding: The coding of position information is positioned after the embedding of both encoder and decoder, and before each block. It is critically important; without it, the model cannot function. Positional Encoding is a unique mechanism of the transformer, compensating for the Attention mechanism’s inability to capture the position information of tokens in a sequence. It allows the positional information and the semantic information (embedding) of each token to be thoroughly integrated and conveyed into the expressions of sequences that have undergone complex transformations.
• Mask Mechanism: Mask refers to masking some values, preventing them from affecting parameter updates. There are two types of masks in the Transformer model, namely padding mask and sequence mask. The padding mask is required in all scaled dot-product attention, while sequence mask is only used in the decoder’s self-attention.
• Padding Mask: Given that each batch’s input sequence length may vary, it’s necessary to align the input sequences.
  • Specifically, this involves padding shorter sequences with 0;
  • If the input sequence is too long, it involves truncating the left part of the content and directly discarding the excess.
  • Attention mechanisms should not focus on these, thus these positions’ values are added with a very large negative number (negative infinity); hence, after softmax, the probabilities of these positions will be close to 0.
• Sequence Mask: Ensures that the decoder cannot see future information. For a sequence, at time_step t, the decoding output should only rely on outputs before time t and not on outputs after t. Therefore, it’s necessary to mask the information after t. This results in creating an upper triangular matrix with all zeros in the upper triangle. This matrix is applied to each sequence.
• Residual Network:

Network degradation phenomenon: Under the precondition that neural networks can converge, as the depth of the network increases, the performance of the network first gradually increases to saturation and then rapidly declines.

In the transformer model, both the encoder and decoder have 6 layers. To ensure that the model can still achieve good training effects when it has many layers, a residual network is introduced. Addresses the network degradation issue caused by excessive depth

Advantages

Two pain points of the Seq2Seq model:

1. The issue of semantic disappearance in long sequences.
2. Loss of positional information.

• Firstly, it addresses the above two issues by: 1-Residual structures, 2-Position encoding.
• Multi-head attention extracts more information.
• Multiple heads of attention in the encoder layer can be computed in parallel.
• The self-attention module allows the source and target sequences to “self-associate” first, enriching the information contained in the embedding representations of the source and target sequences.
• The FFN layer also enhances the model’s expressive capability.
• …

7. RNN

SRN

In Feedforward Neural Networks, layers are connected between each other, but not internally (no cyclical connections); both input and output lengths are fixed, making it incapable of handling sequences of variable lengths.

$$h_{t}=f(Uh_{t-1}+Wx_{t}+b)$$ Turing completeness refers to a set of data manipulation rules that can implement all the functionalities of a Turing machine and solve all computable problems. All Turing machines can be simulated by a fully connected recurrent network composed of neurons that use the sigmoid activation function.

A Bi-directional RNN is essentially two RNNs put together, one reads a sentence (sequence) forwards, and the other reads it backwards, thus, the output of each node contains information from the entire sentence.

Long Term Dependency Problem

The problem of exploding and vanishing gradients, which can only learn dependencies over short periods. Exploding Gradients Weight Decay: A regularization technique aimed at limiting the complexity of the model. It is achieved by adding a regularization term to the model’s loss function, which is usually a penalty of the model weight’s L2 norm. The purpose of this penalization is to prevent the model weights from becoming too large, thereby reducing the model’s complexity and suppressing overfitting. Gradient Clipping: Clipping gradients exceeding a threshold (e.g., >15 equal to 15) Vanishing Gradient Problem Changing recurrent edges to linear dependencies: $h_{t} = h_{t-1}+g(X_{t};\theta )$ - This actually also solves the long-term dependency problem. Adding non-linearity (residual structure): $h_{t}= h_{t-1}+g(X_t,h_{t-1};\theta)$

The two structural improvements for the vanishing gradient issue are essentially what LSTM does. LSTM can alleviate the problem of vanishing gradients but does not solve the problem of exploding gradients (even more severely, due to being more complex). Regarding the LSTM exploding gradient issue, the explanation provided by Li Hongyi is: unlike typical situations where the vanishing gradient is caused by the sigmoid function, the vanishing gradient in RNNs is due to the same parameter being reused multiple times, much like $x^n$, where a slight change in $x$ could lead to a significant change in the result. The reason LSTM mitigates vanishing gradients is due to cell memory, which changes the recurrent edge from multiplication to addition, making the impact of memory persistent (unless the forget gate acts), resulting in longer-lasting memory.

LSTM

LSTM networks introduce a gating mechanism to control the paths of information transmission. The three “gates” are the input gate $i_t$, the forget gate $f_t$, and the output gate $o_t$, which serve the following purposes:

• The forget gate controls how much information from the previous internal state $c_{t-1}$ needs to be forgotten (retained).
• The input gate controls how much information from the current candidate state $\tilde c_t$ needs to be saved (input).
• The output gate controls how much information from the current internal state $c_t$ needs to be output to the external state $h_{t}$.

Advantages of LSTM over RNN:

The disadvantage is still the gradient explosion!

Advantages of RNN:

• Has memory capability, can process and predict time series data. Disadvantages of RNN:
• When dealing with long sequences, RNN’s performance is poor because as the information propagation distance increases, gradient propagation is likely to experience the problems of gradient vanishing or explosion.
• RNN’s parameter update speed is slow because backpropagation needs to wait for the output of the previous moment.
• RNN’s model capacity is small because the path of information propagation is short, making it difficult to capture long-term dependency information. Advantages of LSTM:
• Can handle long sequence information because LSTM stores long-term dependency information in memory units, allowing for longer information propagation paths.
• LSTM updates parameters faster because the memory unit stores long-term dependency information, enabling quicker parameter updates.
• LSTM has a larger model capacity because the memory unit stores long-term dependency information, allowing better capturing of sequence information. Disadvantages of LSTM:
• Although LSTM can handle long sequences, its performance on shorter sequences is not as good as that of RNN.

GRU

The essence of the Gate Recurrent Unit is: the old does not go, the new does not come. The input and output gates are linked; when the input opens, the output closes and vice versa - each time replacing with fresh data.

Seq2Seq ???

Specific Applications:

Formula Representation:

Synchronous:

Asynchronous:

8. Network Optimization

Difficulties in Network Optimization

Structural differences No universal optimization algorithm Many hyperparameters Non-convex optimization problems Parameter initialization Escaping local optima Vanishing gradients, exploding gradients

Non-convex optimization problem in low-dimensional space: there are some local optima and parameter initialization issues. Non-convex optimization problem in high-dimensional space (deep neural networks): the issue is not about escaping local optima but about saddle points. Saddle points have a first-order gradient of zero but the Hessian matrix is not semi-definite.

In high-dimensional spaces, local minima require to be the lowest point in every dimension, which is highly improbable, meaning, in high-dimensional spaces, most stationary points are saddle points. Stochastic gradient descent is very important for non-convex optimization problems in high-dimensional spaces as introducing randomness in the gradient direction can effectively help to escape saddle points.

When a model converges to a flat local minimum, it tends to be more robust, i.e., minor parameter changes will not significantly affect the model’s capacity; whereas, when a model converges to a sharp local minimum, its robustness is comparatively poorer. In network training, it’s unnecessary to find the global minimum, as this might lead to overfitting.

Improvements in Neural Network Optimization:

• Optimization Algorithms
  • Dynamic Learning Rate Adjustment
  • Gradient Correction Estimation
• Parameter Initialization Methods, Preprocessing Methods
• Modifying Network Structure to Optimize the Terrain
• Hyperparameter Optimization

Optimization Algorithms

Impact of Batch Size

Batch size does not affect the expectation of the stochastic gradient, but it does affect the variance of the stochastic gradient;

• Large batch - Small stochastic gradient variance - Stable - Larger learning rate

Learning Rate Adjustment

Learning Rate Decay

Learning Rate Warmup

In mini-batch gradient descent, when the batch size is set to be relatively large, it usually requires a larger learning rate. However, at the beginning of training, because the parameters are randomly initialized, the gradients tend to be large as well, and a larger initial learning rate can make the training unstable. Therefore, it is necessary to start with a smaller learning rate, and then gradually increase (warmup) it. After the warmup is over, the learning rate can decay again

$$\alpha_{t}= \frac{t}{T}\alpha_{0}$$ where $T$ is the number of iterations for warmup

Periodic learning rate adjustment, including cyclic learning rate, restarts, etc., all follows a pattern of first increasing and then decreasing within a cycle, with an overall downward trend. This strategy can cope with sharp minima and flat minima to find local optima.

Adaptive Learning Rate Adjustment

$\alpha$ represents learning rate, $\beta$ decay rate, and $\epsilon$ exists to prevent division by zero Adagrad has the problem of monotonically decreasing learning rates RMSProp changes the computation of $G_t$ from accumulation to exponential decay moving average, so the learning rate is no longer monotonically decreasing

Gradient Optimization

Momentum

$$\Delta\theta_{t}=\rho\Delta\theta_{t-1}-\alpha g_{t}$$ where $\rho$ is the momentum factor, generally set to 0.9, $\alpha$ is the learning rate, and parameter update $\theta_t = \theta_{t-1} +\Delta \theta_t$ The actual update difference for each parameter depends on the weighted average of the gradients over a recent period. When the gradient directions of a parameter are inconsistent in the recent period, the actual update magnitude of the parameter decreases (end of the training); conversely, when the gradient directions are consistent, the actual update magnitude of the parameter increases, acting as an accelerator (beginning of the training).

Nesterov Accelerated Gradient

$$\theta = \hat \theta - \alpha g_{t}$$ $$\hat \theta = \theta_{t-1}+\rho \Delta \theta_{t-1}$$ In the easy-to-misunderstand version offered by Tang Dynasty: $$\Delta \theta_{t} =\rho \Delta \theta_{t-1}-\alpha g_{t}(\theta_{t-1} +\rho \Delta \theta_{t-1}) $$ The actual version:

The difference between them is: Momentum uses the gradient at point $\theta_{t-1}$, while NAG uses the gradient at point $\hat \theta = \theta_{t-1}+\rho\Delta \theta_{t-1}$.

Nesterov completes the journey of Momentum in one step, therefore, it is considered “accelerated”.

Adam

Adam ≈ RMSProp + Momentum

1. First, calculate two moving averages $$M_{t}= \beta_{1}M_{t-1}+(1-\beta_{1})g_{t}$$ $$G_{t}=\beta_{2}G_{t-1}+(1-\beta_{2})g_t^2$$
2. Bias correction $$\hat M_{t} = \frac{M_{t}}{1-\beta_{1}^{t}}$$ $$\hat G_{t} = \frac{G_{t}}{1-\beta_{2}^{t}}$$
3. Update $$\Delta \theta = -\frac{\alpha}{\sqrt{\hat G_{t}+\epsilon}}{\hat M_t}$$

Gradient Clipping

Threshold clipping $$g_{t}= max(min(g_{t},b),a)$$ Clip by norm $$g_{t} = b\frac{g_{t}}{\vert \vert g_{t} \vert \vert }$$

Parameter Initialization

• Pre-training
• Random initialization
  • Gaussian distribution (Normal)
  • Uniform distribution
• Fixed value initialization

Data Preprocessing

Data Normalization

Max-min Normalization Max-min Normalization $$\hat x = \frac{x-min}{max-min}$$ Standardization $$\hat x = \frac{x-\mu}{\sigma}$$ Whitening and PCA After whitening, the features have low correlation with each other, and all features have the same variance. PCA is a major implementation approach.

Batch Normalization and Layer Normalization

$$\hat x = \frac{x-\mu}{\sqrt{\sigma^{2}+\epsilon}}\gamma + \beta$$ This is how it is calculated, but the target is different:

Batch normalization is done across different samples, while layer normalization is done within the same sample. Batch normalization normalizes a single neuron across different training data, whereas layer normalization normalizes among all neurons within the same layer of a single training datum.

Question

Problem 7-8 Analyze why batch normalization cannot be directly applied to recurrent neural networks.

Answer

Layer normalization can be applied to RNNs, as shown the differences below

• Batch normalization normalizes a single neuron in an intermediate layer, thus requiring a batch size that is not too small; otherwise, it is difficult to calculate the statistical information of a single neuron (too few samples lack statistical significance).
• If the distribution of an input to a neuron dynamically changes within a neural network (such as in RNNs), then batch normalization cannot be applied.
• Layer normalization normalizes all neurons in an intermediate layer, making it suitable for RNNs.

Title

Refer to the following formula

Answer

1. 𝑓(BN(𝑾𝒂(𝑙−1) + 𝒃)) represents the batch normalization performed after linear computation and before nonlinear activation (that is, net input 𝒛(𝑙))
2. 𝑓(𝑾BN(𝒂(𝑙−1)) + 𝒃) indicates the batch normalization performed on the output of the previous layer, before the linear computation of the current layer

By using the first type of batch normalization, it is possible to prevent changes in distribution caused by linear computation

Dropout

Dropout: When training a deep neural network, we can randomly drop a portion of neurons (and their corresponding connections) to avoid overfitting.

During training, the average number of activated neurons is 𝑝 times of the original. During testing, all neurons can be activated, leading to inconsistent outputs between training and testing. To alleviate this issue, during testing, the neuron layer’s input 𝒙 should be multiplied by 𝑝, which is equivalent to averaging different networks. The retention rate 𝑝 can be determined through the validation set for an optimal value. Generally, for hidden layer neurons, a retention rate 𝑝 = 0.5 works best, effective for most networks and tasks. With 𝑝 = 0.5, during training, half of the neurons are dropped, leaving only the other half activated, creating the most diverse network structures. For input layer neurons, the retention rate is usually set to a number closer to 1 to ensure the input changes are not too drastic. Dropping input layer neurons, equivalent to adding noise to the data, enhances the network’s robustness.

This PowerPoint is still incorrect. In Xi Peng Qiu’s book, it’s $2^n$ subnetworks, but he inadvertently changed it to 2n 😅

The Bayesian interpretation suggests: Dropout is a sampling of the parameter $\theta$.

Variational Dropout: When applying Dropout to RNNs, one should not drop the recurrent connections but should randomly drop the non-recurrent connections. Random drops should be done for each element of the parameter matrix, using the same dropout mask at all times.

Try to analyze why directly applying dropout on the recurrent connections of recurrent neural networks is not feasible? Randomly dropping the hidden states at each time step would damage the recurrent network’s capability to remember across the time dimension.

9. Deep Reinforcement Learning

Five Elements

The basic elements of reinforcement learning include:

1. State 𝑠 is the description of the environment, which can be either discrete or continuous, with its state space denoted as 𝒮.
2. Action 𝑎 is the description of the agent’s behavior, which can be either discrete or continuous, with its action space denoted as 𝒜.
3. Policy 𝜋(𝑎|𝑠) is the function by which the agent decides the next action 𝑎 based on the current environmental state 𝑠. (mapping from state to action)
4. State transition probability 𝑝(𝑠′|𝑠, 𝑎) is the probability of the environment transitioning to state 𝑠′ in the next time step after the agent takes an action 𝑎 based on the current state 𝑠.
5. Immediate reward 𝑟(𝑠, 𝑎, 𝑠′) is a scalar function. It is the reward fed back to the agent by the environment after it takes an action 𝑎 based on the current state 𝑠. This reward is often related to the state 𝑠′ in the next time step.

Markov Processes

Markov Process (Markov Process) is a sequence of random variables $𝑠_0, 𝑠_1, ⋯，𝑠_𝑡 ∈ 𝒮$ with Markov property, where the state at the next moment $𝑠_{𝑡+1}$ depends only on the current state $𝑠_𝑡$, $$𝑝(𝑠_{𝑡+1}|𝑠_𝑡, ⋯ , 𝑠_0) = 𝑝(𝑠_{𝑡+1}|𝑠_{t}),$$ Markov decision process introduces an additional variable into the Markov process: the action $𝑎$, the state at the next moment $𝑠_{𝑡+1}$ not only relates to the current state $𝑠_𝑡$ but also to the action $𝑎_𝑡$, $$𝑝(𝑠_{𝑡+1}|𝑠_𝑡,a_t, ⋯ , 𝑠_0,a_0) = 𝑝(𝑠_{𝑡+1}|𝑠_{t},a_t),$$ where $𝑝(𝑠_{𝑡+1}|𝑠_{t},a_t)$ is the state transition probability.

In Markov processes, there are no actions and rewards, while Markov decision processes consider both actions and rewards

Given a policy $𝜋(𝑎|𝑠)$, one trajectory $\tau$ (Trajectory) of the Markov decision process $$\tau = 𝑠_0, 𝑎_0, 𝑠_1, 𝑟_1, 𝑎_1, ⋯ , 𝑠_{𝑇−1}, 𝑎_{𝑇−1}, 𝑠_{𝑇 }, 𝑟_𝑇$$ The probability of obtaining this trajectory is: $$p(\tau )= p(s_0)\prod_{t=0}^{T-1}\pi(a|s)p(s_{t+1}|s_{t},a_{t})$$ If there are no termination states in the environment, the total reward for the trajectory is: $$G(\tau ) = \sum\limits_{t=0}^{T-1}\gamma^tr_{t+1}$$ where $\gamma \in [0,1]$ is the discount rate, when $\gamma$ is close to 0, the agent cares more about the short-term reward; when $\gamma$ is close to 1, the long-term reward becomes more important. Unless specified otherwise, use $\gamma =1$. The objective function of reinforcement learning is to maximize the expected return.

Learning Methods Based on Value Functions

State value function: given a state $s$, the expected return from executing policy $\pi$

$$V^{\pi}(s) =\mathbb E{{\tau \sim p(\tau)} }{[\sum\limits{t=0}^{T-1}\gamma^{t}r_{t+1}\vert \tau_{s_{0}}= s]}$$

The expected return of a policy $\pi$ (the expectation of all possible trajectories, the expectation of the value of all states reachable from $s$) $$\mathbb E{\tau}{[G(\tau)]} = \mathbb E{{s\sim p(s_0)}}[V^{\pi}(s)]$$ Transitioning from $s$ to $s^\prime$, there is the Bellman equation, $$V^{\pi}(s) = \mathbb E{{a\sim\pi(a|s) }}\mathbb E{{s’\sim p(s’|s,a) }}[r(s,a,s^\prime)+\gamma V^{\pi}{(s^{\prime})}]=\sum\limits_{a\in A}\pi(a|s)(R_{s}^{a}+{\gamma}\sum\limits_{s’\in S}P_{ss’}^{a}V^{\pi}(s’))$$ Think of a Markov chain to facilitate memorizing this formula. Inside, $\pi(a|s)$ is the policy, which is the probability distribution of actions $a$ taken in state $s$, $p$ is the probability distribution of the state $s$ possibly reaching state $s’$.

Q function: In more detail, the expected total return for taking action $a$ in state $s$, and then following policy $\pi$: $$Q^{\pi}(s,a) = \mathbb E{{s’\sim p(s’|s,a) }}[r(s,a,s^\prime)+\gamma V^{\pi}{(s^{\prime})}]=\sum\limits{s’\in S}P_{ss’}^{a}(R_s^a+\gamma V^{\pi}{(s^{\prime})})$$ This is essentially fixing the action $a$ in the Bellman equation. The state value function $𝑉^𝜋(𝑠)$ is the expectation of the Q function $𝑄^𝜋(𝑠, 𝑎)$ over action $a$, i.e., $V^{\pi}(s) = \mathbb E_{a\sim \pi (a,s)}{[Q^{\pi}(s,a)]}$, substituting into the above formula, we get the Bellman equation for the Q function: $$Q^{\pi}(s,a) = \mathbb E_{s’\sim p(s’|s,a)}{[r(s,a,s’)+\gamma \mathbb E_{a’ \sim \pi(s’,a’)}{[Q^{\pi}(s’,a’)]}]}$$

Dynamic Programming Methods

Both methods are model-based reinforcement learning (learning with a model), where the model is a Markov Decision Process (MDP). Two limitations:

• The model must be known, that is, the state transition probability 𝑝(𝑠′|𝑠, 𝑎) and reward function 𝑟(𝑠, 𝑎, 𝑠′) must be given. However, this requirement is hard to meet in practical applications (Solution: random walk to explore the environment).
• State space is large, resulting in extremely low efficiency (Solution: neural network approximation for V (Deep Belief Q-Network)).

Policy Iteration

Policy iteration consists of policy evaluation (calculating $V^{\pi}(s)$) and policy improvement (simple greed).

Value Iteration

It is equivalent to iterating $V^{\pi}(s)$ only, without iterating the policy, directly generating at the end.

Monte Carlo Methods

Monte Carlo (sampling) methods: When the state transition probability 𝑝(𝑠′|𝑠, 𝑎) and reward function 𝑟(𝑠, 𝑎, 𝑠′) are unknown, the MDP model collapses (model-free reinforcement learning), requiring sampling to compute the Q function. $$Q^{\pi}(s,a) = \frac{1}{N}\sum\limits_{n=1}^{N}G(\tau^{n}{s_0=s,a{0=a}})$$ The Q function is approximated through the average return of N experimental trajectories. $\epsilon$-greedy method: select other actions in $\mathbb A$ with probability $\epsilon$ (very small), with each action being selected with probability $\frac{\epsilon}{\vert \mathbb A \vert}$

Temporal Difference Methods

This is an on-policy method. Monte Carlo methods require a complete path to know its total return and do not rely on Markov property; while temporal difference learning methods only need one step, and its total return is estimated through the Markov property.

Q-Learning

Is an off-policy temporal difference method. Different from the SARSA algorithm, Q-learning does not select the next step’s action $𝑎′$ through $\pi^\epsilon$, but directly selects the optimal Q function. Thus, the updated Q function is about policy $\pi$, not $\pi^\epsilon$.

Actor-Critic

10. Level 20 real questions

Short Answer Questions

1. CNN computation

Input image is 97*97*3, with 15 9*9 filters, no padding, step stride of 2. (1) Compute the output image size (5 points) (2) The number of parameters in this convolutional layer (5 points) (3) Characteristics of CNNs (5 points)

2. Self-Attention Mechanism

······ChatCPT·····Musk·······Dangerous AI······ (1) Structure diagram of self-attention (5 points) (2) If calculating similarity using dot product, provide the complete calculation process for self-attention (10 points)

3. Explanation of Theorems

Explain the No Free Lunch theorem and the Ugly Duckling theorem separately (10 points)

4. Optimization Algorithms

Discuss momentum method and Nesterov Accelerated Gradient (10 points)

5. Optimization Algorithms

Explain the difficulties and focus points of parameter optimization in high and low dimensions (10 points)

Short Answer Questions

1. Describe the SGD (Stochastic Gradient Descent) algorithm, and list its advantages and disadvantages (10 points)
2. LSTM is an improvement over RNN, can it solve the problems of gradient vanishing and exploding? Please explain the principle (15 points)

Essay Question

….Xpeng G6’s autonomous driving is impressive….Assuming you are an algorithm engineer for Xpeng, please model the human-machine interaction system of Xpeng vehicles using deep reinforcement learning, list the five elements of reinforcement learning, and provide an algorithm for maximizing the reward function. (15 points)

Yes, a dialogue system based on deep reinforcement learning;